유니온 파인드, 최소 신장 트리, 백준 1197번 파이썬

1. 유니온 파인드

개요

일반적으로 여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union 연산과

두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성된 알고리즘

union, find 연산을 완벽히 이해하는 것이 핵심

• union 연산: 각 노드가 속한 집합을 1개로 합치는 연산. 노드 a, b가 a { A, b { B일 때 union(a,b)는 A U B를 말함.
• find 연산: 특정 노드 a에 관해 a가 속한 집합의 대표 노드를 반환하는 연산. 노드 a가 a { A 일때 find(a)는 집합의 대표 노드를 반환

구현 방법

1차원 리스트 이용

1. 노드가 연결되어 있지 않으므로 각 노드가 대표 노드가 됨. 1차원 리스트를 자신의 인덱스값으로 초기화.

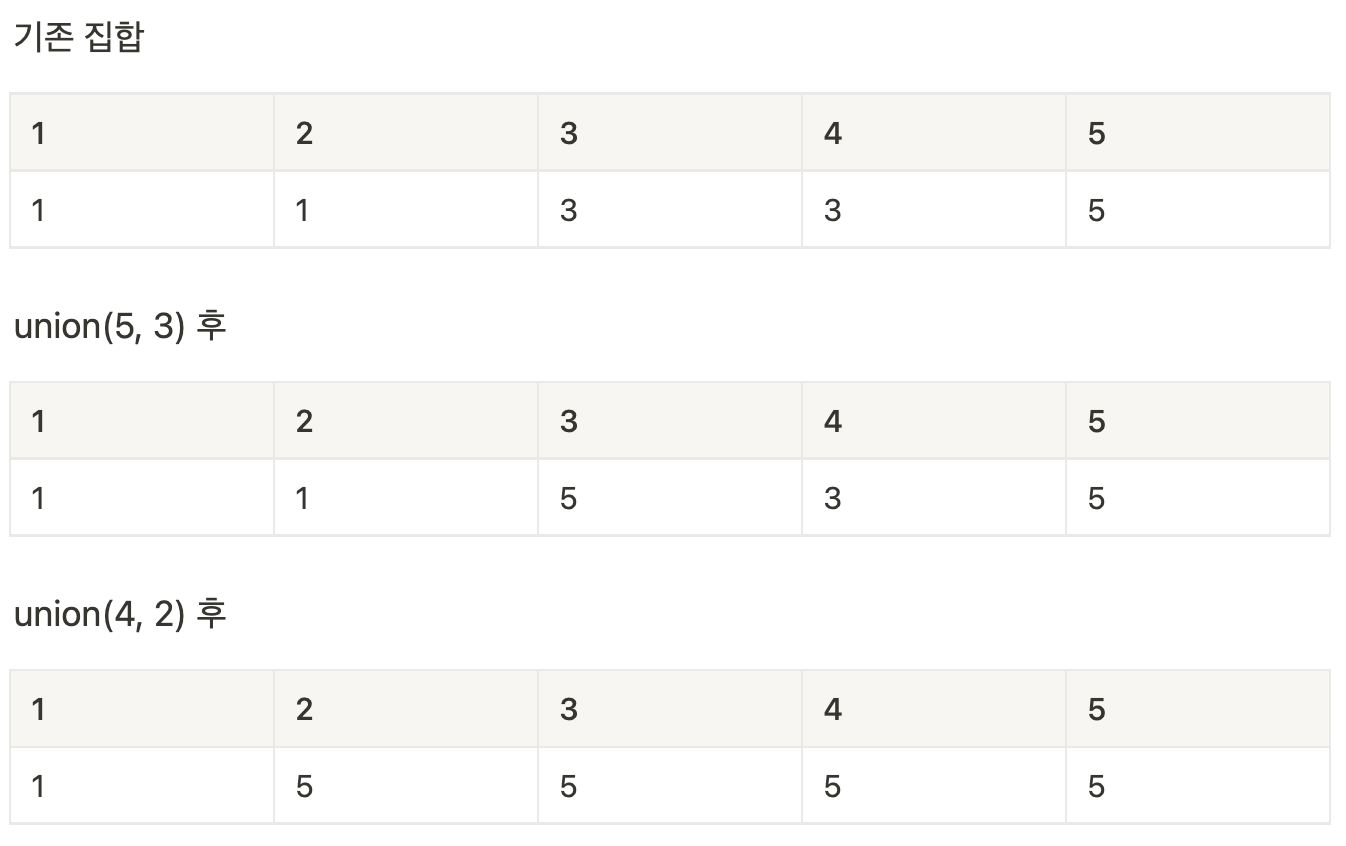
• union 연산
  • 각 노드가 속한 집합을 1개로 합치는 연산.
  1. union(a, b)할 시 a, b 각각의 대표 노드값 find연산으로 찾아, 대표 노드 두개 중 하나의 값으로 변경.
• find 연산
  • find역할 외에도 그래프 정돈 및 시간 복잡도 감소.
    • 경로 압축 효과: 여러 노드를 거쳐야 하는 경로에서 그래프를 변형해 더 짧은 경로로 갈 수 있도록 함으로써 시간 복잡도를 효과적으로 줄이는 방법.
  1. 대상 노드 리스트에 index값과 value값이 동일한지 확인.
  2. 동일하지 않으면 value값이 가리키는 index위치로 이동.
  3. 이동 위치의 index값과 value값이 같을 때까지 1~2를 반복. 재귀 함수로 구현.
  4. 대표 노드(index = value)에 도달하면 재귀 함수를 빠져나오면서 거치는 모든 노드값을 대표 노드값으로 변경.

조심해야 할 것

1. find 연산 구현 시 재귀를 나오면서 대표 노드값으로 설정
2. union 연산 구현 시 find 사용하여 대표 노드끼리 연결

 

2. 최소 신장 트리(minimum spanning tree)

개요

주어진 그래프의 모든 노드를 연결하는 부분 그래프 중,

사용된 에지들의 가중치의 합을 최소로 하는 트리.

특징

• 사이클이 포함되면 가중치의 합이 최소가 될 수 없으므로 사이클을 포함하지 않는다.
• N개의 노드가 있으면 최소 신장 트리를 구성하는 에지의 개수는 항상 N-1개이다.

에지 리스트를 이용해 구현한다.

 

에지 리스트

에지를 중심으로 그래프를 표현. 에지 정보를 단순하게 [출발 노드, 도착 노드, 가중치]의 형식으로 리스트 안에 집어넣는다.

• 구현하기 매우 쉬움(단순히 리스트에 에지 정보를 넣으면 됨)
• 특정 노드와 관련되어 있는 에지를 탐색하기 어려움.
• 노드 중심 알고리즘에는 잘 사용하지 않음
• 리스트에 출발 노드 도착 노드를 저장하여 에지를 표현. EX) [[1, 2], [2, 3]]
• 가중치가 있다면 나 추가로 가중치를 저장. EX) [[1, 2, 3], [2, 3, 2]]

 

최소 신장 트리 구현 방법

1. 에지 리스트로 그래프를 구현하고 유니온 파인드 리스트 초기화.
   1. 노드 변수 2개와 가중치 변수로 구성된 리스트 제작.
   2. 사이클 처리를 위해 노드 당 유니온 파인드 리스트도 함께 초기화.
2. 그래프 데이터를 가중치 기준으로 정렬.
   1. 에지 리스트에 담긴 그래프 데이터를 가중치 기준으로 오름차순 정렬.
3. 가중치가 가장 낮은 에지부터 연결 시도.
   1. 바로 연결하는 것이 아니라 find연산으로 사이클이 유무를 확인.
      1. 두 노드의 대표 노드가 서로 같다면 사이클이 만들어짐.
   2. 형성되지 않을 경우에만 union연산을 이용해 두 노드를 연결.
4. 전체 노드 개수가 N개이면 연결한 에지의 개수가 N-1이 될때까지 과정 3 반복.
5. 총 에지 비용 출력하기.

 

백준 1197

import sys
V, E = map(int, input().split())
e_list = [[] for i in range(E)]			# 그래프는 에지 리스트로 구현
n_list = [i for i in range(V + 1)]		# 유니온 파인드용 노드 리스트

for i in range(E):
    e_list[i] = list(map(int, input().split()))

e_list.sort(key=lambda x: x[2])

def union_find(a):		# find 연산 구현
    if a == n_list[a]:	# 자신이 집합의 대표값(index == 값)일 때 반환
        return a
    else:
        represent_node = union_find(n_list[a])	# 재귀로 돌아오면서 업데이트
        n_list[a] = represent_node
        return represent_node


cnt = 0
answer = 0

def union(a, b, w):		# 유니온 시 가중치 업데이트
    global cnt
    global answer
    a = union_find(a)
    b = union_find(b)
    if a != b:
        cnt += 1
        answer += w
        n_list[b] = a

idx = 0
while cnt < V-1:
    union(e_list[idx][0], e_list[idx][1], e_list[idx][2])
    idx += 1

print(answer)