1. 다익스트라 알고리즘
개요
그래프에서 최단 거리를 구하는 알고리즘 입니다. 특정 출발 노드에서 다른 노드로 가는 최단 거리를 모두 구하기 때문에 출발 노드가 고정되어 있을 때 사용 가능합니다. 추가적으로 에지들의 가중치 또한 항상 양수여야 합니다.
| 기능 | 특징 | 시간 복잡도(노드 수: V, 에지 수: E) |
| 출발 노드와 모든 노드 간의 최단 거리 탐색 | 에지는 모두 양수 | O(ElogV) |
구현 방법
간단하게 말하자면 BFS로 탐색을 진행하되, 다음 탐색 지점을 방문하지 않은 노드 들 중 가장 가까운 곳부터 선택하도록 하는 방법입니다.
위와 같이 항상 갈 수 있는 가장 최솟값인 경로만 택함으로써 결과적으로 각 노드는 출발 노드로부터 최단 경로만에 도달하게 됩니다.(간선의 가중치가 모두 양수가 아니라면 돌아올수록 비용이 줄어드므로 모두 양수여야 합니다.)
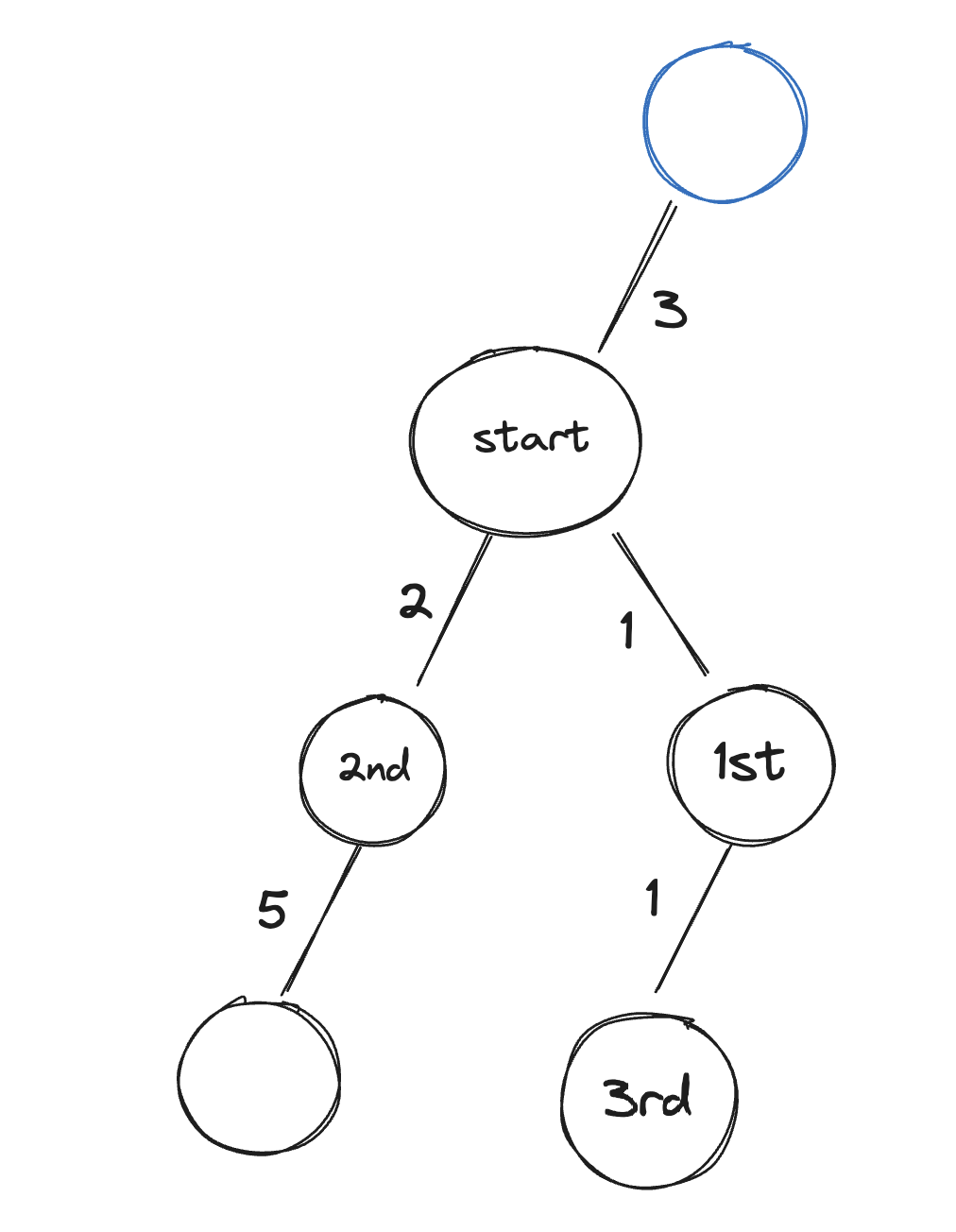
- 인접 리스트로 주어진 그래프를 구현합니다.
- 다른 노드까지의 최단 거리를 저장하는 리스트를 하나 만들고 초기화
- 출발 노드는 0, 이외의 노드는 무한으로 초기화합니다. 무한은 적당히 큰 값을 사용합니다.
EX) 주어진 모든 에지의 합보다 충분히 더 큰 수
- 출발 노드는 0, 이외의 노드는 무한으로 초기화합니다. 무한은 적당히 큰 값을 사용합니다.
- 현재 도달한 노드를 가지고 있는 큐에서 값이 가장 작은 노드를 선택합니다(우선순위 큐를 이용).
- 초기에는 0인 출발노드에서 시작하게 됩니다
- BFS를 돌듯이 방문 리스트를 만들어 처리(값이 가장 작은 노드를 선택하므로 최단 거리를 보장)합니다. 단, 방문 순서는 최단 거리를 기준으로 우선순위 큐에서 뽑힌 순서입니다.
- 뽑힌 노드가 아직 방문하지 않은 노드인지 확인하고 방문하지 않았을 시 방문 처리 후 이후 과정을 진행합니다.
- 특정 노드의 최단 거리가 갱신될 때마다 큐에 이미 있더라도(기존 원소를 갱신하기보다는) 다시 넣게 되기 때문에 이미 방문했을 가능성이 있습니다.
- 해당 노드가 연결된 에지들을 가져와 방문하지 않았을 경우 최단 거리 리스트를 업데이트하고 업데이트 될 경우 우선순위 큐에 추가합니다.
- 방문했을 경우, 이미 3번 설명과 같이 최단거리가 완성된 상태입니다.
- 선택된 노드에 연결된 에지의 값을 바탕으로 다른 노드의 값을 업데이트 합니다.
- min(선택 노드의 최단 거리 리스트의 값 + 에지 가중치 -> 새롭게 생성된 값, 연결 노드의 최단 거리 리스트 값 -> 기존 최단 거리)
EX) min(shortest_path_list[cur_node_num] + len_edge, shortest_path_list[new_node_num] )
- 모든 노드 처리시까지(우선순위 큐가 빌 때까지) 3~5를 반복합니다.
- 3번 과정에서 방문하지 않은 노드 중 항상 거리값이 가장 작은(최단 거리인) 노드를 뽑았기 때문에, 에지 가중치가 양수라면, 그 값은 항상 해당 노드까지 가는 최단거리입니다.
- 4번 과정에서 새롭게 발견된 노드까지의 최단 거리를 기준으로 다른 기존 노드들도 업데이트 해주므로 어떤 경우에도 최단 거리가 보장됩니다.
백준 1753
https://www.acmicpc.net/problem/1753
import sys
input = sys.stdin.readline
print = sys.stdout.write
from queue import PriorityQueue
my_pq = PriorityQueue()
V, E = map(int, input().split())
n_list = [[] for i in range(V+1)]
sp_list = [5*(10**7) for i in range(V+1)]
v_list = [False for i in range(V+1)]
s_node = int(input())
for i in range(E):
u, v, w = map(int, input().split())
n_list[u].append([v, w])
# 인접 리스트 만들기 종료
sp_list[s_node] = 0
my_pq.put((0, s_node))
while not my_pq.empty():
cur_node = my_pq.get()[1]
if not v_list[cur_node]:
v_list[cur_node] = True
for new_node_set in n_list[cur_node]:
new_node = new_node_set[0]
if not v_list[new_node] and sp_list[new_node] > sp_list[cur_node] + new_node_set[1]:
sp_list[new_node] = sp_list[cur_node] + new_node_set[1]
my_pq.put([sp_list[new_node], new_node])
for i in range(1, V+1):
if sp_list[i] != 5*(10**7):
print(str(sp_list[i]) + "\n")
else:
print('INF\n')
'컴퓨터 공학 분야 별 지식 > 개념(파이썬)' 카테고리의 다른 글
| 최단거리 찾기 2 - 벨만-포드(bellman-ford-moore) 파이썬, 백준 11657 파이썬 (1) | 2024.03.18 |
|---|---|
| K번째 최단 거리 찾기 파이썬, 백준 1854 파이썬 (1) | 2024.03.11 |
| 유니온 파인드, 최소 신장 트리, 백준 1197번 파이썬 (1) | 2023.10.29 |
| 우선순위 큐(Priority Queue)와 그리디 알고리즘(Greedy) 파이썬, 백준 1715 파이썬 (1) | 2023.10.28 |
| 큐(queue), BFS(너비 우선 탐색), 트리의 지름, 백준 1167 파이썬 (1) | 2023.10.26 |